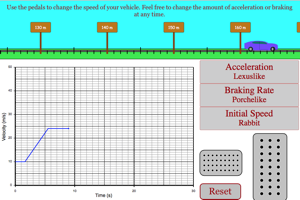
When you press on the gas pedal the car will accelerate, when you let off the gas the car will move at a constant speed. Look at the graph of velocity vs. time when the car is accelerating and when the car is moving at a constant speed. Change the car type and see how the velocity vs. time graph changes as you accelerate. Build up speed and then hit the break pedal. Notice the change that takes place for the velocity-time graph. Click on the title of the y-axis to change your graph to a position vs. time graph. Make sure you understand how the graphs illustrate the behavior of the car.

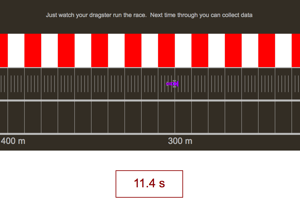
Collect data as the car is covering the 400 m course. Plot a graph of position vs. time and notice that the trip is composed of two distinct types of motion. Make sure you understand what is happening for each type of motion and that you can find the top speed of the car.

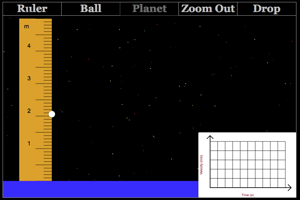
Zoom in on the planet and drop the ball. Click on the velocity-time graph to zoom in to measure the acceleration of the ball as it fell. Change properties of the ball. How do different properties of the ball affect the gravitational acceleration of the ball? Now change properties of the planet. Measure the new acceleration of the ball. How do different properties of the planet affect the gravitational acceleration of the ball?

Play around with launching fireworks to remind yourself of some of the main ideas with vertical motion. Think about what is happening to the speed of the firework on the way up, on the way down and at the highest natural point of its flight. How does changing the gravitational field affect the nature of the flight of the firework. How does the initial speed affect the maximum height?

Adjust different properties of the system and see how the gravitational force changes as a result of this alterations.

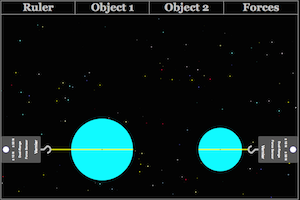
What factors determine the strength of the gravitational force between two masses? How does increasing the distance between centers affect the force of gravity? How does increasing either mass affect gravity?

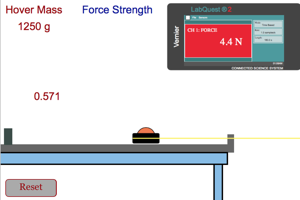
Notice the shape of the position-time graph of the hover craft as it is pulled across the table. What does this show us about the craft as it was moving? Look at the velocity-time graph. What specific thing can we determine from the slope of this graph? How does the amount of force applied to the craft and the mass of the craft affect the slope of this graph.

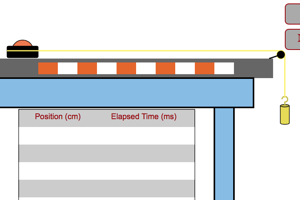
This lab is similar to the previous lab on Newton's Law, but with one huge difference. In the previous lab a person was pulling the craft across the table and in this lab a mass hanging over the pulley is causing the acceleration. Why would the two situations not give the exact same acceleration even though they might have the same applied force and the same mass for the hovercraft?

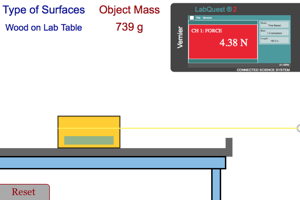
When you hit the start button the person will begin pulling the mass to the right. The mass does not initially move because of friction. As time goes on the person will gradually increase the force until the object starts to move. They will then apply just enough force to keep the object at a slow and steady speed. As you look at the graph below the action, make sure you understand why the horizontal line is lower than the peak force. Why did the person want to make sure that the object was moving at a steady speed once it started it's motion? What factors determine the force needed to keep the object moving? What was this applied force equal to?

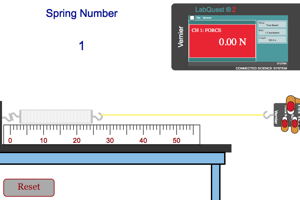
Look at the graph after the spring has stopped stretching. What must the applied force be equal when the spring is held in this position? What are the factors that affect the amount of force needed to hold the spring in a certain state of stretch?

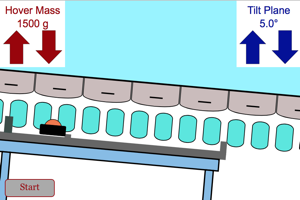
Incline your plane by a slight angle. Release the hover puck and then look at the graphs given below the action pane. Notice the shapes of the position-time and velocity-time graph. Use the velocity-time graph to get the acceleration of the craft. Change the mass of the craft to see how the mass affects this acceleration.

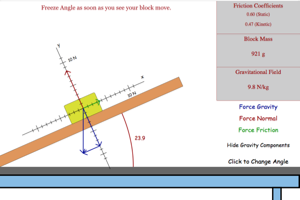
Click to start the inclination of your plane. Notice the magnitude and direction of each of your forces. Notice how the size of the forces change with angle. Notice what happens to force friction when the box stats to move. Try changing the mass of the box to see how it affects the slip angle for the box. Try changing the gravitational field to see how it affects the slip angle for the box.

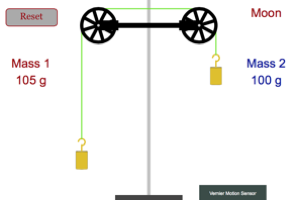
Play around with different combinations of masses on the two sides of the Atwood machine. Try to keep the total mass constant and see how the difference in mass affects the system. Then try to keep the difference in mass constant but vary the total mass. How does the total mass of the system affect its motion?

Play around with a few of the variables in this program to see how they affect the stopping distance for the car. As always, make only one variable change at a time. Try doubling the speed and seeing what happens to stopping distance. Try doubling mass and see how that affects stopping distance. Try a few different combinations of surfaces and see how they affect stopping distance.

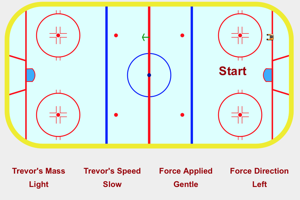
The most important thing to learn from this program is how the direction of the force relative to the motion of the object affects the type of motion that they object undergoes. Which force direction, relative to the object's motion, will not affect the KE energy of the object?

The questions for this activity are already included as part of the activity. Try to get an intuitive feel for all the ways of discussing circular motion as you go through this program.

This simulation gives idealized results for horizontal circular motion for a stopper on a string. There is one major difference between the motion the stopper in this program and the motion of a stopper in the real life version of this lab. What is the major difference between the stopper in this program and the stopper motion in real life?

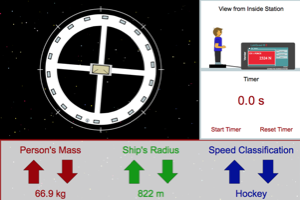
Why do we see space stations like the one in this program spinning when they are depicted in movies or on tv? How does each of the parameters you control in this program affect what the person on the station experiences because of this spinning?

A car traveling too quickly when it reaches a turn will lead toward unfortunate results. Try to create a situation in which the car is going too fast. Explain the situation in terms of Newton's laws. Find the limits for a car on a turn. Pick a set of conditions and try to see what is the maximum speed you could take the turn. How does varying the different parameters affect this speed?

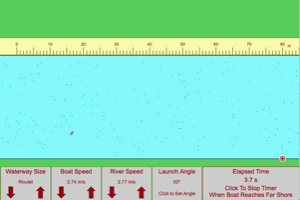
Launch your boat so its motion in still water would have carried it directly across the river. The river current will carry it down stream. How much time does the boat require to cross the river? How far downstream does the boat go? Now change the speed of the river. How are each of your answers affected by the speed of the river?

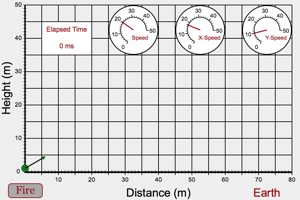
Fire few projectiles from a height of about 20 m with an angle of 0°. How does the speed of the projectile affect the distance it travels and the time it is in the air? Bring the starting location of the projectile back to the ground. Fire the projectile at a bunch of different angles and note how long it stays in the air and how far it goes horizontally. Which angle is best for time in air and which angle is best for horizontal distance traveled? Try 30° and 60°. What do you notice about the distance traveled?

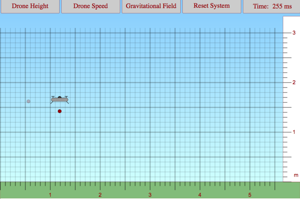
Play around with this program to find the relationships that govern the behavior of a package that has been released by a drone that is flying horizontally. You will have control over the drone's height and horizontal speed. You will also be able to adjust the gravitational field in the region where the drone is flying. You want to make sure that you understand how the time of flight and the horizontal displacement of the projectile are affected by each of the parameters that you have control over.

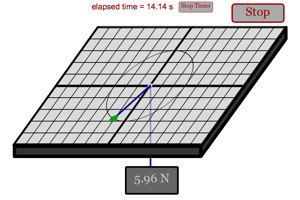
How do each of the different parameters affect the force needed to hold the puck in a circular path on the frictionless table?

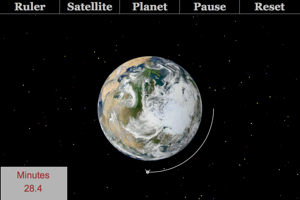
How does the mass of the satellite affect the orbital period? Switch over to a custom planet. How does the mass of the planet affect the orbital period? How does the radius of the planet affect orbital period (make sure you don't change the radius of the orbit but only the radius of the planet. You can do this by shrinking the planet's radius instead of increasing it.) How does the orbital radius affect the orbital period?

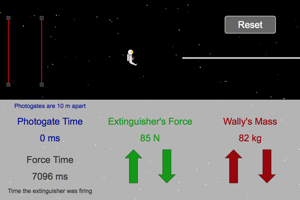
What are the two factors that determine the impulse given to Wally in this program? Calculate the momentum of Wally while moving through the photogates and compare it to the impulse you gave him before he reached the gates. Make sure you shut off the fire extinguisher before he reaches the first gate.

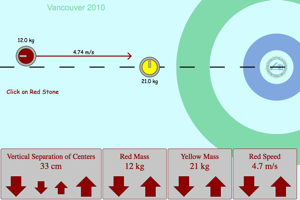
Set the two stones so that they have equal masses. Make the vertical separation between the stones 0 cm. Collide the stones and notice the behavior of the stones during the collision. Make the red stone heavier than the yellow stone and collide them again. Make the yellow stone heavier and collide them again. Notice how the masses of the stone relative to one another change the result of the collision. Change the vertical separation and collide them a few more times. Notice how the stones separate.

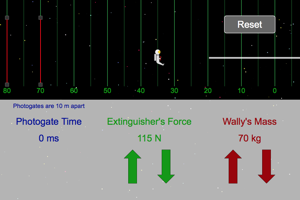
Fire the extinguisher for a certain distance and then use that distance to find the work done by the fire extinguisher to Wally. Calculate the KE of Wally while he was moving through the photogates. What conclusion can we draw about the work done and the KE gained by Wally?

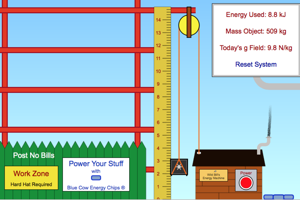
Add some cow chips to your machine and then use it to lift an object from the ground to some height. Calculate the PEg gained by the object you are lifting. How does this relate to the energy used by the machine (the work)? Why was it important that the machine lifted the object at a steady speed?

How can you determine the work done in stretching the spring using the graph that is produced below the action window? What can you learn by taking the slope of this graph?

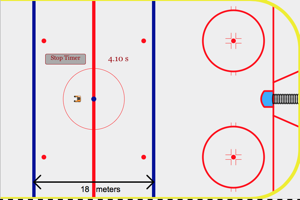
Fire Trevor down the ice and as this firing is happening think about the energy transformations that are happening. What kind of energy does Trevor posses at the moment before he is fired? What type of energy does he posses after leaving the spring? Make sure you can calculate both of these energy types. When you try these calculations you should find the energy before he starts moving equal to the energy after he leaves the spring. You will need to time Trevor's motion through the neutral zone to find one of your types of energy.

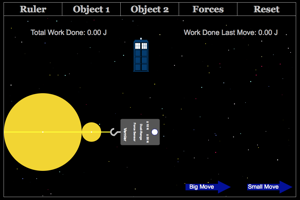
Why does the formula for gravitational potential energy, mg∆h, not work for a situation like the one depicted in this program. Use the universal gravitational energy formula to calculate the energy when your object is on the surface of the heavenly body and then calculate it again after you move it some distance away from the heavenly body. How do you use your two numbers to find the work done by the force to move your object from its starting location to its ending location.

This lab is designed to have students investigate the amount of energy lost by a ball when it bounces. Students will change the starting height of the ball and see how this affects the amount of energy lost and the percent of the original energy lost.

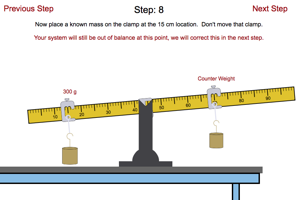
Try working through this lab to determine the mass of the unknown that will be added to your system in the last step of the lab.

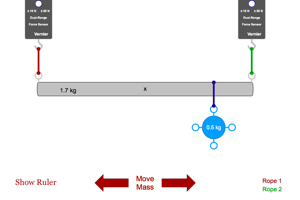
Try moving the mass to different locations on your suspension bridge. How does the force tension in each rope change when the mass is in different locations? What is always the same about the two tensions, regardless of where the mass is located?

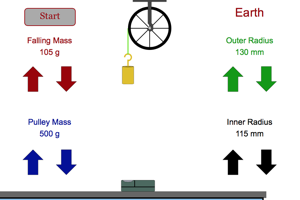
The only factor you should change in this experiment is the size of the inner radius of the pulley. Start by having the inner radius as large as possible and allow the mass to fall toward the motion sensor. Look at the graphs for position vs. time and velocity vs. time. Make sure you understand why they have the shape that they do. Get the slope of the velocity vs. time graph. Now drop the inner radius to zero so that you are using a pulley that is the same mass as in the first trial but with the mass spread out evenly in a disk instead of all concentrated near the outside. Again get the slope of the velocity vs. time graph. Think about how the location of the pulley mass affected its inertia.

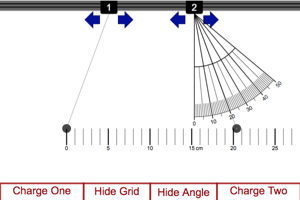
Adjust the different factors and notice how the angle of displacement from the vertical changes. This angle is a result of the force on the charge and can be used as a gauge as to how much force is on the charge.

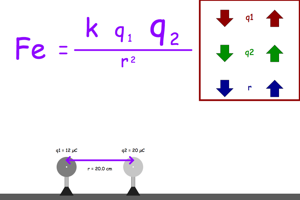
Adjust the different factors and note their affect on the force between the two charges.

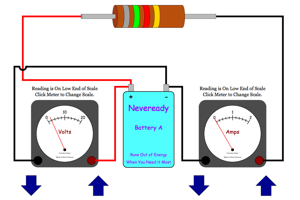
Notice how current is affected by voltage and resistance.

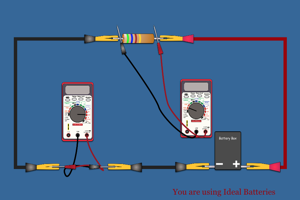
Notice how the current is affected by the voltage of the batteries and the resistance of the resistor. Click on the battery box to get the voltage (each battery adds another 1.5 V). Click on the resistor to get its colors and hence its resistance.

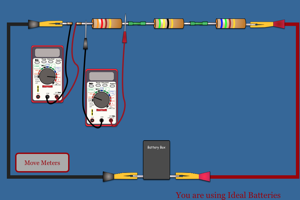
What is true of the current in this series circuit? What is true of the voltage lost in the resistors compared to the total voltage of the battery pack? Click on the battery box to get the voltage (each battery adds another 1.5 V).

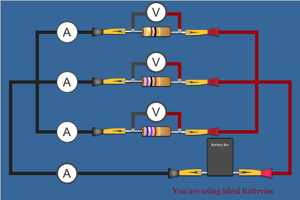
What is true of the current in this parallel circuit? What is true of the voltage lost in the resistors compared to the total voltage of the battery pack? Click on the battery box to get the voltage (each battery adds another 1.5 V).

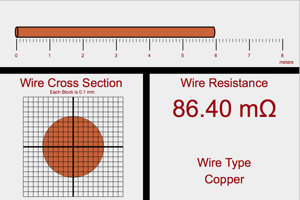
What are the three factors that determine the resistance of a wire? How does each factor contribute to determining the resistance of the wire?

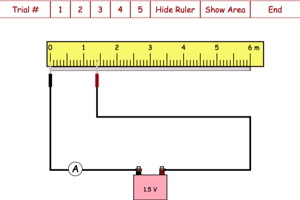
This lab is designed to have students work through a procedure that will allow them to determine the resistivity of a wire based on the amount of current going through different lengths of wire.

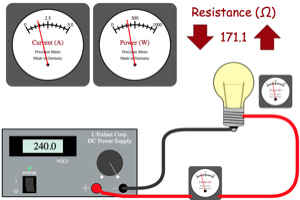
Adjust one parameter at a time and see how that parameter affects the amount of power delivered to the light bulb.

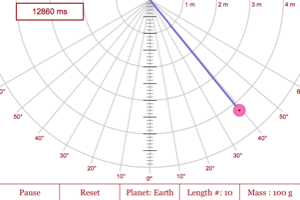
Explore the factors that do (and don't) affect the period of a pendulum. As you are watching your pendulum swing, think about the type of energy it possesses at the different points. How does the total energy of this pendulum change over time? How about for a real pendulum? Why is there a difference (that is, what has been eliminated from the system in this program that would exist in real life)?

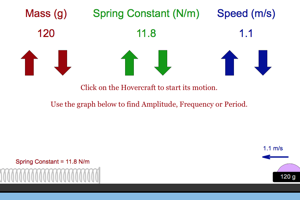
If the spring constant of the spring in this system was a known value, we could use the oscillations of the system to determine the mass of the object that is oscillating. The value of the mass determined in this way is often referred to as the inertial mass because this method of determining mass does not depend on gravity and would work as well on an orbiting space station as it does on Earth.

Compare the graph produced in this lab with the one produced in the previous lab. What is different and think of some reasons for this difference? Which of the two more closely resembles real objects in the real world.

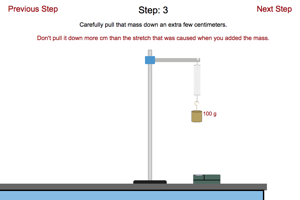
Work your way through this lab and see if you can determine the mass of the unknown object that is added to the spring at the last step.

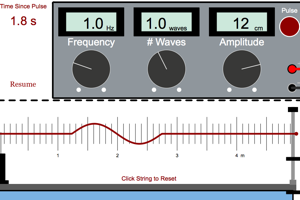
Send just 0.5 of a wave down the string and make sure you understand the difference between the way the waves reflect off the clamp when the string is tied tightly to the clamp and the way they reflect then the string is attached to a light ring that is free to move. Then set your generator to make 1.0 wave. How does frequency affect the wavelength of the wave. How does the tension in the string affect the wavelength of the wave? How does the linear density of the wave affect the wavelength of the wave?

Play around with this program and make sure you understand what conditions lead to constructive interference and destructive interference. Try creating some crazy wave patterns and then pause the program before they overlap. Try to predict the shape of the combined wave. Resume the program and watch the waves interfere in slow motion. Did your predictions match reality?

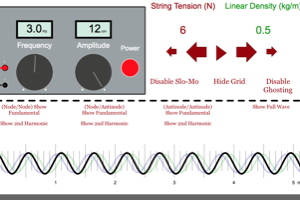
This program combines a wave move from the right with a wave moving from the left. These waves will have identical frequencies and amplitudes. When they combine they will form standing waves. Activate the ghosting feature and the slow motion feature and make sure you understand the resulting wave that occurs from the individual waves. Can you find nodes and antinodes? How do the different changeable parameters help determine the distance between these nodes and antinodes?

Activate the different fundamental and 2nd harmonics features to see how a standing wave with this wavelength would look on a string with fixed ends and moveable ends. Relate the space available to the wave to its wavelength. Make sure you know how this will apply to musical instruments.

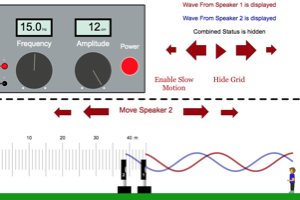
When you first turn on your generator the two sound waves will travel the same distance before reaching you. How far back must you move the speaker to create destructive interference at the place you are listening to the wave? How far back must you move the speaker to create constructive interference at the place you are listening to the wave? There is more than one answer to these questions so make sure you understand the pattern of distances that will create destructive interference and the pattern that will create constructive interference.

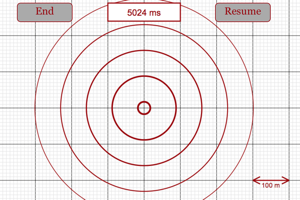
Play around with this program and make sure you can find the wavelength of a wave based on the picture of the wave fronts. How does the frequency of the wave creation and the speed of the wave affect this wavelength? What happens to the intensity of the wave as it moves farther from the source? Is this a violation of energy conservation.

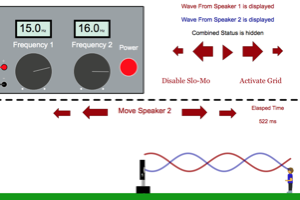
With f1 = 15 Hz and f2 = 16 Hz, start the sound flowing. Notice how the synchronization of the waves changes with time and place. Determine the beat frequency by looking at the number times you go from constructive interference to destructive interference and back to constructive interference per second. Will the separation distance between the speakers have any effect on the beat frequency? Why are beats heard best when both waves have the same amplitude? Why is the beat frequency for humans capped around 7 Hz?

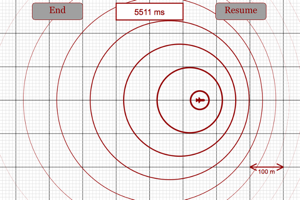
Make sure you understand the wave patterns created by a source that is at rest, a source that is moving slowly to the right, a source that is moving quickly to the right, a source that is traveling at the speed of the waves, and a source that is traveling faster than the waves.